📈 Processing ! Un carnet de croquis numérique adapté aux sciences

nov.

2021

📈 Processing ! Un carnet de croquis numérique adapté aux sciences

😤 Ce billet a été édité le : 2023-09-30

Processing est un carnet de croquis numérique flexible et un langage pour apprendre à coder dans le contexte des arts visuels.

ඏ

Présentation de Processing

C’est un excellent outil pour :

Jouer avec des algorithmes célèbres comme le « jeu de la vie » de John Conway – « Game of Life », John Conway, 1970,
Explorer l’univers des fractales
- du flocon de Koch inventée en 1904 par le mathématicien suédois Helge von Koch,
- l’ensemble de MandelBrot et l’Ensemble de Julia découvert par les mathématiciens Gaston Julia et Pierre Fatou en 1918.

Ensemble de Julia (Définition)

L’ensemble de Julia est construit à l’aide de la formule suivante :

$\begin{aligned} Z_{0} = z et Z_{n + 1} = Z_{n}^{2} + C \end{aligned}$

où Z et C appartient à l’ensemble de complexes et C est une constante.

Ensemble de Julia (Code)

/*
** Julia.pde - Java Julia by MN Karthik.
** Any questions, comments, suggestions? You can contact me at mnkarthik@yahoo.com.
**
** Modifications and adaptation to Processing by Mad Merv 2004 - www.madmerv.com
** Adaptation Claude CHOISNET 2021 to last processing version.
*/

void setup() {
  background(0);
  size(600, 600);
}

void draw() {
  int sx=width;         // Screenwidth
  int sy=height;        // Screenheight
  double xmin=-(1.5);   // smallest real value (x-axis)
  double xmax=(1.5);    // largest real value (x-axis)
  double ymin=-(1.5);   // smallest imaginary value (y-axis)
  double ymax=(1.5);    // largest imaginary value (y-axis)
  double maxiter=512;   // Max number of iterations

  double old_x;         // temporary variable to store x-value
  double fx, fy;
  double ix=0.42;       // C Constant real part
  double iy=0.23;       // C Constant imaginary part
  int m;                // variable to store number of iterations

  double dx=(xmax-xmin)/sx; // how much to add for each x-pixel?
  double dy=(ymax-ymin)/sy; // how much to add for each y-pixel?

  int px;           // Variable storing current x-pixel
  int py=0;         // Variable storing current y-pixel
  double x;         // Variable storing current x-value
  double y=ymin;    // Variable storing current y-value

  stroke(0);
  while (py<sy) {
    px=0;
    x=xmin;
    py++;
    while (px<sx) {
      px++;

      fx=x;
      fy=y;
      m=0;
      do {
        old_x=fx;
        fx= fx*fx - fy*fy + ix;
        fy= 2*old_x*fy + iy;
        m++;
      } while (((fx*fx+fy*fy)<4) && (m<maxiter));
      stroke(m%50+((mouseX+mouseY)/2), m%12*(255/12), m%4*(255/4));
      line(px-3, py-3, px+10, py+10);
      x+=dx;
    }
    y+=dy;
  }
  stroke(0);
}

Voici une représentation graphique de l’ensemble de Julia pour C = 0.42 + 0.23i

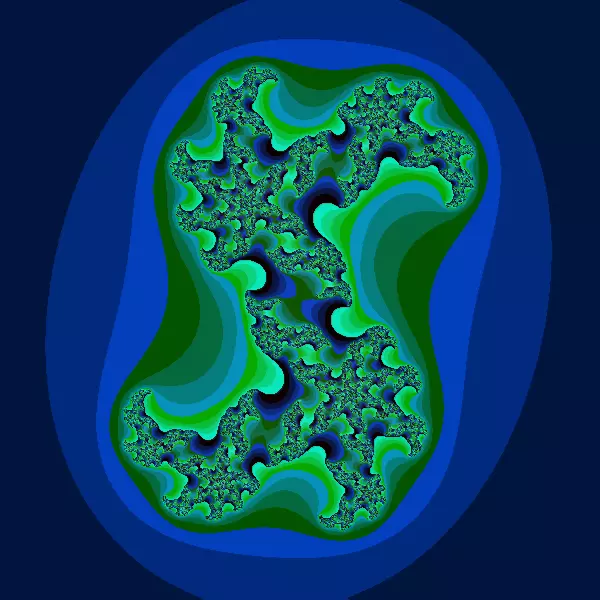
Bon, on peut commencer par moins hardcore…

Processing intègre de nombreuses fonctionnalités :

Exportation au format DXF: un format permettant d’échanger avec d’autres applications de CAO ou de DAO,
Exportation au format PDF,
Exportation au format SVG,
Accès aux entrées-sorties de votre ordinateur sur Raspberry Pi et autres Linux,
Échanges réseaux : permettant de recevoir ou d’envoyer des données sur Internet,
Support de l’interface série (RS-232),
Le son : en sortie comme en entrée,
la vidéo : récupération d’image depuis votre caméra, lecture de fichiers vidéos ou exportation vidéos.

L'outil est prévu pour manipuler simplement des objets en 2D ou en 3D.

ඏ

Usages

C’est l’outil pédagogique parfait permettant créer simplement des animations ou des images d’illustrations.
C’est un outil bien adapté aux étudiants comme aux enseignants.

ඏ

Un exemple « simple »

Non, en fait, ce n’est pas simple, mais en réalité la partie lourde du code est liée à la décoration (l’affichage de la grille principalement).

Pour utiliser ce code, vous n’aurez qu’à modifier ce que retournent les 2 premières fonctions.

Ici, on cherche à résoudre le système d’équation suivant :

Y = 2X + 1
Y = -(X²) + 4

qu’il faudra traduire comme suit :

return 2.0*x +1.0;
return -( x * x ) + 4.0;

Si vous souhaitez utiliser un autre système d’équations, il suffit d’adapter les 2 lignes correspondantes.

Bon presque, car il reste encore à s’assurer que la solution se trouve dans l’espace d’affichage…

Le code correspondant

Dans un cadre pédagogique, il est possible de mettre le code concernant l'affichage dans une autre classe, et de limiter le code au strict minimum.

// USER FUNCTION
float y1(float x) { // The function to plot
  // return 2.0 * x * x -8.0;
  return 2.0*x +1.0;
}

float y2(float x) { // The function to plot
  return -( x * x ) + 4.0;
}

//______________________________________________________________________
void setup() {
  size(1000, 500); // SIZE OF SCREEN
  noLoop();
}

void draw() {
  background(255);
  draw_grid();
  translate(width/2, height/2);
  draw_functions();
}

//______________________________________________________________________
// can be other TAB..
final int steps = 100;
float X, Y1, Y2, Xo=0, Y1o, Y2o;
final float f_start_x = -10, f_stop_x = 10;
final float dx = (f_stop_x - f_start_x )/float(steps);
final float epsilon = 1;

//consts
final color RED  = color(255, 0, 0);
final color BLUE = color(0, 0, 255);

void draw_functions() {
  strokeWeight(1);
  for ( int i = 0; i< steps; i++) {
    X = f_start_x + dx * i;
    if ( i == 0 ) Xo=X;                      // need a dummy init for first line
    Y1 = y1(X);
    if ( i == 0 ) Y1o=Y1;
    Y2 = y2(X);
    if ( i == 0 ) Y2o=Y2;
    if ( abs(Y2 - Y1) <= epsilon ) {
      println("solution near i "+i+" X "+nf(X, 1, 2)+" Y1 "+nf(Y1, 1, 2)+" Y2 "+nf(Y2, 1, 2));
    }

    // draw it: // in processing draw y negativ! // scale to GRID by w
    stroke(RED);
    line(Xo*w, -Y1o*w, X*w, -Y1*w);
    circle(X*w, -Y1*w, 2);
    stroke(BLUE);
    line(Xo*w, -Y2o*w, X*w, -Y2*w);
    circle(X*w, -Y2*w, 2);

    // remember for next loop draw line
    Y1o = Y1;
    Y2o = Y2;
    Xo = X;
  }
}

final int x = 0, y = x, w = 25, h = w, offset = 0;
void draw_grid() {
  // grid of rectangles
  int gridx = width / w;
  int gridy = height / h;
  //int many = gridx*gridy;
  noFill();
  stroke(0);
  for (int i = 0; i < gridx; i++) {
    for (int j=0; j <gridy; j++ ) {
      rect(x+i*(w+offset), y+j*(h+offset), w, h);   // or any other shape/text on that position
    }
  }
  // add
  // https://discourse.processing.org/t/math-and-processing/9292/7 @CHRISIR
  // small lines with numbers ||||||||||| : for x axis
  pushMatrix();
  translate(width/2, height/2);
  strokeWeight(3);
  textSize(15);
  textAlign(CENTER);
  fill(0); // BLACK
  stroke(0); // BLACK
  for (int i = -gridx/2 + 1; i < gridx/2; i++) {
    float dx = 1;
    float X =  dx * i;
    if (X==0) {
      continue;  // skip this number
    }
    float xToDraw = getXtoDraw(X);
    float yToDraw = getYtoDraw(0);
    line(xToDraw, yToDraw, xToDraw, yToDraw+11);
    text( i, xToDraw-1, yToDraw+29-1);
  }//for
  textAlign(LEFT);
  strokeWeight(1);
  popMatrix();

  // small lines with numbers : for y axis
  pushMatrix();
  translate(width/2, height/2);
  stroke(0); // BLACK
  fill(0);  // BLACK
  textSize(15);
  textAlign(CENTER);
  strokeWeight(3);

  for (int i = -gridy/2 + 1; i < gridy/2; i++) {
    float dx = 1;
    float Y =  dx * i;
    if (Y==0 || Y==-1) {
      continue;  // skip these numbers
    }
    float xToDraw = getXtoDraw(0);
    float yToDraw = getYtoDraw(Y);
    line(xToDraw, yToDraw, xToDraw+11, yToDraw);
    text(i,
      xToDraw+24, yToDraw);
  }

  textAlign(LEFT);
  strokeWeight(1);
  popMatrix();
  // show arrows and texts X and Y
  decoration();
  fill(255);
  ellipse(width/2, height/2, 5, 5);       // show center point
}

void decoration () {
  stroke(0);
  strokeWeight(3);

  // vertical line
  line ( width/2, 0, width/2, height);

  // horizontal line
  line ( 0, height/2, width, height/2);

  // texts X and its arrow ---
  fill(0);
  textSize(24);
  text ( "X", width-17, height/2+31);

  pushMatrix();
  noFill();
  strokeWeight(3.0);
  strokeJoin(MITER);
  beginShape();

  float f = 3.0;
  translate(width-f*7, height/2);
  vertex(3.5*f, -3.0*f);
  vertex(6.5*f, 0.0*f);
  vertex(3.5*f, 3.0*f);
  endShape();
  strokeWeight(1);
  popMatrix();

  // texts Y and its arrow ---
  fill(0);
  textSize(24);
  text ( "Y", width/2+10, 22);
  pushMatrix();
  noFill();
  strokeWeight(3.0);
  strokeJoin(MITER);
  beginShape();
  translate(width/2, 22);
  vertex( -3.0*f, -3.5*f);
  vertex( 0.0*f, - 6.5 * f);
  vertex( 3.0*f, - 3.5 * f);
  endShape();
  popMatrix();
}

// ---------------------- HELPER FUNCTIONS ----------------------

float getXtoDraw(float xin_) {
  return xin_*w;
}

float getYtoDraw(float yin_) {  // in processing draw y negativ!
  return -yin_*w;
}
//

ඏ

Installation

Pour les plateformes classiques, vous trouverez tout ici : https://processing.org/download.

Installation Linux 64 bits

cd ~/Downloads/
wget https://github.com/processing/processing4/releases/download/processing-1277-4.0b2/processing-4.0b2-linux64.tgz

tar xvf processing-4.0b2-linux64.tgz
cd ~/Downloads/processing-4.0b2
./install.sh

La dernière version ne fonctionne pas sur Raspberry PI. Le support des machines 32 bits semble avoir été abandonné, et la version Linux 64bits ne fonctionne pas sur un processeur ARM. Après avoir fait quelques essais, je pense que c’est finalement que très temporaire. Puisque c’est la cross-compilation qui semble être la limite actuelle (le fait de compiler depuis un couple (système,architecture) vers un autre couple (système,architecture)). Les versions 32 bits et 64 bits sont de nouveau proposées.

ඏ

Références

Site officiel de Processing,
- Code source de la dernière version sur GitHub,
- Le Code source des versions précédentes étant dans un autre repository.
https://processingfoundation.org/,
Les fractales de Mandelbrot et Julia.
Math and processing
Outil permettant d’afficher des courbes en ligne : desmos

ᦿ

Vos commentaires

Pas encore de commentaire - ajouter le votre.
Ajouter votre commentaire

cClaude.rocks ☕ Le blog

Présentation de Processing

Usages

Un exemple « simple »

Installation

Références